Parallel operations in conventional computing have proven to be an essential tool for efficient and practical computation, and the story is not different for quantum computing. Indeed, there exists a large body of works that study advantages of parallel implementations of quantum gates for efficient quantum circuit implementations.
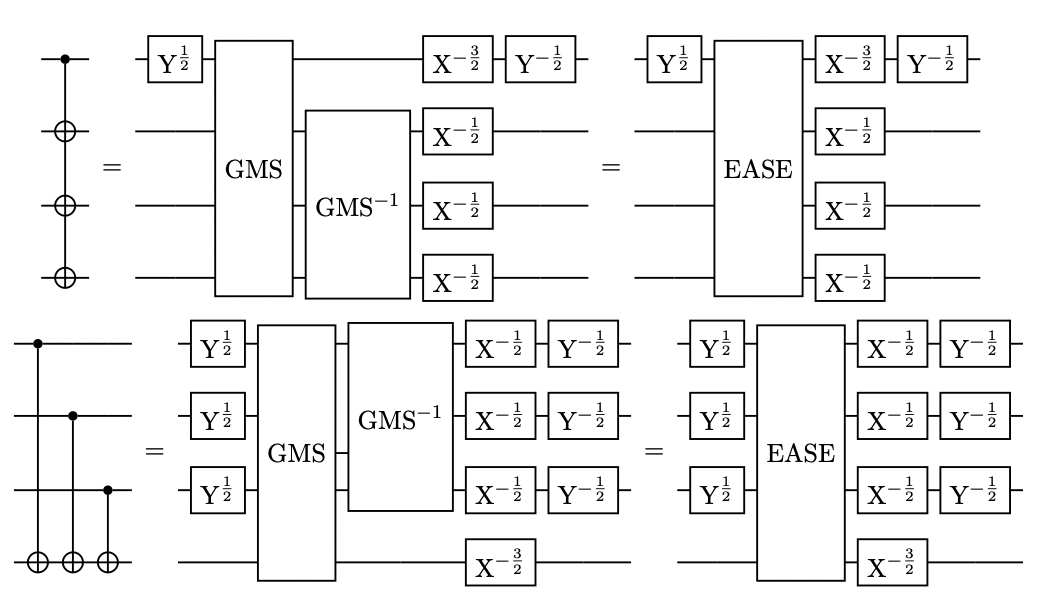
Trapped-ion quantum computers are capable of exotic operations which entangle several qubits at once. One such powerful operation is the Efficient, Arbitrary, Simultaneously Entangling (EASE) gate.
Leveraging its flexibility in selecting arbitrary pairs of qubits to be coupled with any degrees of entanglement, all in parallel, we show an n-qubit Clifford circuit can be implemented using 6 log(n) EASE gates, an n-qubit multiply-controlled NOT gate can be implemented using 3n/2 EASE gates, and an n-qubit permutation can be implemented using six EASE gates.
The researchers showed that EASE gates make it drastically easier to implement circuit elements for universal quantum computation: An n-qubit Clifford circuit can be applied in only 6log(n) EASE gates, an n-qubit multiply-controlled NOT gate in 3n/2 EASE gates, and an n-qubit permutation in only six EASE gates.