Por: Rodrigo Ferreira (Cofundador Brazil Quantum)
Este artigo é para você que, lendo o post da semana passada, ficou se perguntando: “ok, entendi a importância do algoritmo de Grover, mas existem outros algoritmos em computação quântica que eu deveria saber?” A resposta é um retumbante sim e vamos explorar, neste artigo, um dos principais e mais populares algoritmos da literatura.
Algoritmo de Shor

O algoritmo que abordaremos foi desenvolvido pelo matemático americano Peter Shor (atualmente, professor e pesquisador do MIT), nos idos de 1994. Em termos gerais, esse algoritmo trata sobre a fatoração de números naturais sob uma perspectiva extremamente distinta dos métodos clássicos.
Antes de compreender a importância e o impacto do algoritmo de Shor no contexto da computação quântica, é necessário relembrar o porquê de fatoração de números grandes ser tão essencial para as nossas vidas. Como já foi discutido no artigo intrudotório sobre criptografia pós-quântica, decompor um número em fatores primos pode ser uma tarefa mais desafiadora do que se imagina e, por isso, consiste em uma ferramenta útil para criptografar informações.
A fatoração do número 22, por exemplo, pode ser feita mentalmente de forma rápida. Conforme aumentamos o valor, no entanto, nossas mentes não conseguem mais realizar a decomposição e precisamos apelar para os computadores. E o que acontece quando a decomposição desses números é difícil até mesmo para os próprios computadores clássicos? Acontece o surgimento de um dos principais métodos de criptografia já inventados, o RSA. Então, nossos dados estão protegidos para sempre, certo? Basta gerar números cada vez maiores?
Se você já conferiu nosso artigo, sabe que não é bem assim. Além da — amplamente discutida — pesquisa em criptografia pós-quântica, existe um outro ramo chamado criptografia quântica, o qual faz uso de propriedades da matéria em nível quântico para conseguir prover uma distribuição segura de chaves. A Quantum Key Distribution (QKD) é tema de muitas pesquisas e, certamente, é uma vertente que vale a pena acompanhar de perto, pois está trazendo resultados muito interessantes. Mas isso é história para um próximo post.
O problema da fatoração toma um número N como input — o qual possui, digamos, n bits — e, como output, tem dois números a e b (com 1<a,b<N), tais que N=a.b. O algoritmo mais óbvio que conhecemos consiste em testar todos os valores inteiros de 2 até a raiz quadrada de N a fim de encontrar qual deles será o fator de N. Apesar desse algoritmo ter tempo polinomial em N, em n acaba sendo exponencial. Na prática, com algoritmos conhecidos até o momento, inteiros com 1000 ou mais bits são impossíveis de serem fatorados utilizando somente hardware clássico. Agora você entendeu o motivo de usarmos esse problema no RSA?
Ok, chega de contexto. Vamos às contas!
Contas
Seja um inteiro ímpar N, tal que N=ab e tome qualquer inteiro k coprimo com N, isto é, mdc(N,k)=1. É possível mostrar — fica de exercício para o leitor — que existe um valor p tal que:
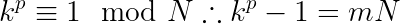
em que m é um inteiro qualquer. Assumindo que p é o menor valor que satisfaz a expressão anterior e fatorando-a, podemos afirmar que N divide a seguinte expressão:
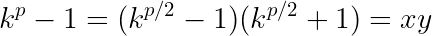
onde x e y correspondem aos valores fatorados da expressão original (diferença de quadrados). Como a diferença |x-y|=2, segue que x e y não possuem fator em comum maior que 2. Uma vez que N foi definido como sendo ímpar, então a é fator de x ou y. Suponha que a seja fator de x, então a divide ao mesmo tempo x e N, ou seja, mdc(x,N)=a.
Para determinar o número p, considere a seguinte sequência em módulo N:
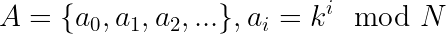
Logo, cada elemento a_i dessa sequência pertence ao conjunto {0,1,…,N-1}. Portanto, existirão índices r e q tais que os valores em módulo N se repetem, isto é:

Se r e q forem os menores valores tais que essa repetição ocorre, é possível mostrar que tomando q=0, então a sequência A vira periódica com período r (faça um exemplo você mesmo para comprovar isso).
Ok, agora basta encontrar o período de A — o que não é fácil, pois nos obriga a testar novamente todos os valores até a raiz de N para encontrar um padrão. Aqui entra uma ferramenta poderosa da computação quântica chamada Transformada de Fourier Quântica, a qual possui uma propriedade muito conveniente para o nosso caso: ela retorna o período de uma entrada periódica. E, com isso, o período r pode ser determinado em tempo polinomial!
Parece mágica, mas como isso é possível? Tome um vetor A de comprimento M e período r, onde r divide M e os elementos são da forma:
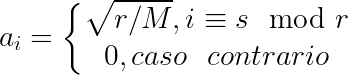
para algum valor s < r. Logo, a transformada de Fourier quântica (QFT) pode ser aplicada:
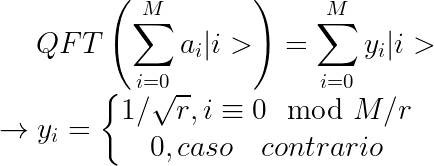
Ou seja, a saída (após a aplicação da QFT) será não-nula em valores múltiplos de M/r. Então, para fatorar um inteiro, basta determinar o período da sequência correspondente utilizando a QFT!
Esperamos que tenha ficado claro o tamanho da vantagem que é utilizar o algoritmo de Shor para o caso de fatoração de números muito grandes. Sair de um cálculo em tempo exponencial — segundo a abordagem clássica — para um outro em tempo polinomial, via Transformada de Fourier Quântica, exige muita inovação e, por isso, a descoberta de Peter Shor é celebrada até hoje como um dos primeiros progressos substanciais dos algoritmos quânticos.