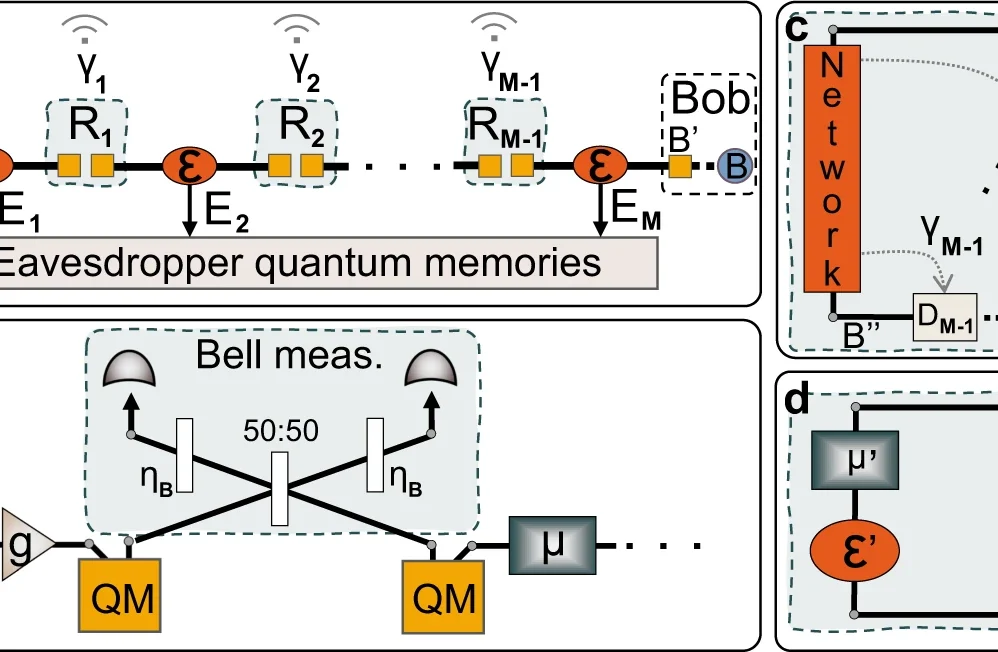
Gaussian networks form a cornerstone of network information theory, facilitating communication between multiple senders and receivers through Gaussian channels. While classical Gaussian networks are well-understood, their quantum counterparts remain an emerging field of study. This research advances the theoretical framework for analyzing the composable security of Gaussian quantum networks with untrusted nodes in finite-size scenarios.
The study addresses the Pirandola-Laurenza-Ottaviani-Banchi (PLOB) bound, a fundamental limit in point-to-point quantum communication. To overcome this bound, researchers have explored quantum repeater chains and network configurations that enable secure communication between multiple user pairs. These developments contribute to the evolution of quantum internet infrastructure for secure communications and distributed quantum computing.
The research focuses on Gaussian quantum networks characterized by Gaussian input signals, quantum channels, and auxiliary devices. The methodology introduces a novel approach to parameter estimation based solely on data shared between end-users, rather than traditional channel parameter estimation. This approach proves particularly valuable for large-scale quantum networks where conventional parameter estimation becomes challenging.
The study demonstrates its findings using a chain of identical quantum links and explores the potential of quantum amplifier-assisted chains. Theoretical results suggest these chains could surpass the repeaterless limit with practical block sizes, though practical implementation presents challenges requiring further investigation.
In the context of continuous-variable quantum key distribution, the research establishes that any two users within a Gaussian quantum network can extract composable secret keys using their local shared data and public information from network stations. The framework accommodates conditionally Gaussian networks, including those utilizing non-deterministic quantum amplifiers, which operate through post-selection mechanisms.
Here are several significant contributions to the field. The team developed a generalized parameter estimation methodology specifically designed for quantum networks. They conducted detailed analysis of composable security within finite-size regimes. The study included thorough investigation of quantum amplifier-assisted chains. Additionally, they created a framework that accommodates conditionally Gaussian networks, expanding the practical applications of their findings.
The research advances our understanding of quantum network security while addressing practical considerations in network design and implementation. These findings have significant implications for the development of quantum internet infrastructure and secure quantum communication systems.
npj Quantum Information, Published online: 08 September 2022; doi:10.1038/s41534-022-00620-5