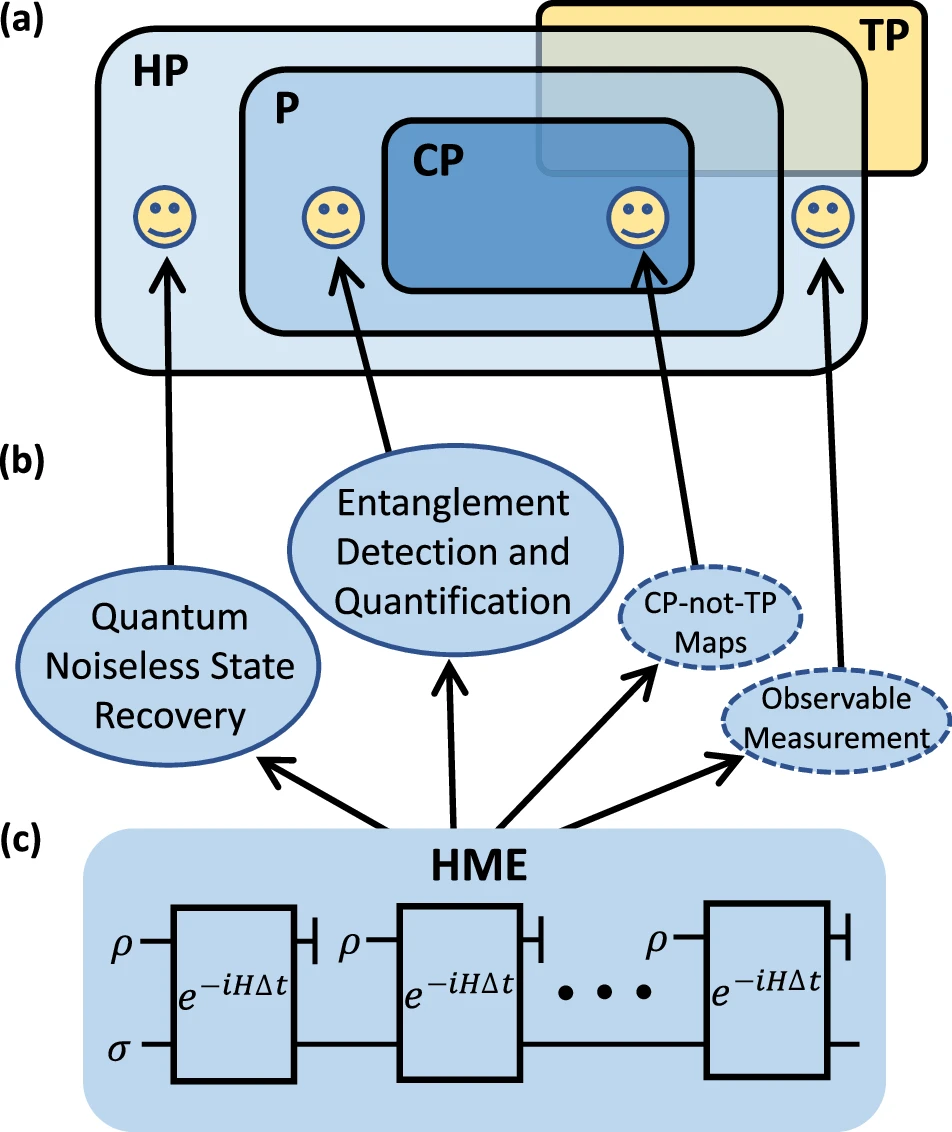
Legitimate quantum operations must adhere to principles of quantum mechanics, particularly the requirements of complete positivity and trace preservation. Yet, non-completely positive maps, especially Hermitian-preserving maps, play a crucial role in quantum information science.
Researchers have introduced the Hermitian-preserving map exponentiation algorithm, which can effectively simulate the action of an arbitrary Hermitian-preserving map by exponentiating its output into a quantum process.
They have analyzed the sample complexity of this algorithm and proved its optimality in certain cases. Utilizing positive but not completely positive maps, this algorithm provides exponential speedups in entanglement detection and quantification compared to protocols based on single-copy operations.
In addition, it facilitates the encoding-free recovery of noiseless quantum states from multiple noisy ones by simulating the inverse map of the corresponding noise channel, providing a new approach to handling quantum noises.
This algorithm acts as a building block of large-scale quantum algorithms and presents a pathway for exploring potential quantum speedups across a wide range of information-processing tasks.
npj Quantum Information, Published online: 30 December 2024; doi:10.1038/s41534-024-00949-z