Discrete Stochastic Processes (DSPs) provide essential frameworks for modeling probabilistic systems across science and engineering. Traditional analysis of DSPs relies on Monte Carlo methods, which face significant challenges as the number of possible realizations grows exponentially with time steps. These methods often require sophisticated importance sampling techniques to reduce variance, particularly when low-probability events carry high impact.
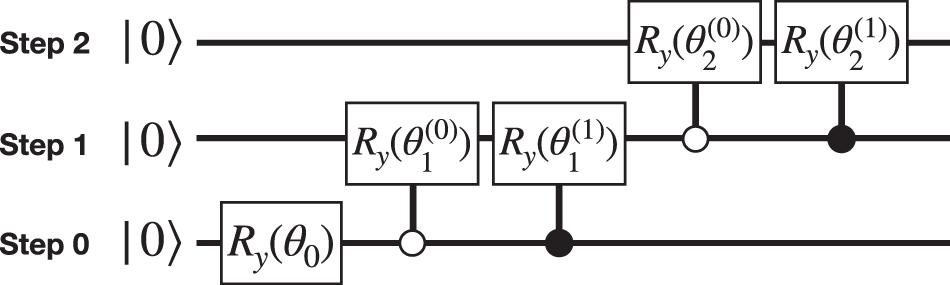
This work introduces a novel quantum algorithm that efficiently calculates the characteristic function of a DSP — which completely defines its probability distribution — using quantum circuit elements that scale linearly with the number of time steps. The approach leverages quantum superposition to simultaneously explore all possible stochastic trajectories, an effect termed “quantum brute force.”
A key innovation maps expectation values onto the probability of measuring a specific computational basis state of a qubit, effectively reducing Monte Carlo sampling to a Bernoulli trial. This provides optimal variance for all sample sizes without requiring specialized sampling strategies, as the method inherently follows the central limit theorem.
The algorithm can be enhanced with quantum amplitude estimation to achieve quadratic speedup in sampling convergence, overcoming classical Monte Carlo limitations. Fourier approximation techniques extend the approach to estimate expectation values for any integrable function of the random variable.
The quantum advantage manifests as both reduced variance and faster convergence for Monte Carlo sampling—or equivalently, smaller sample sizes without precision loss. The method applies to non-identically distributed variables and non-Markovian processes, broadening its applicability.
Practical demonstrations include applications in option pricing theory and correlated random walks, with implications for biology, ecology, and finance. Proof-of-principle experiments conducted on IBM’s quantum cloud platform validate the approach.
While the primary focus is quantum sampling advantage for DSPs, connections exist to quantum memory advantages previously shown for stochastic processes with causal structures and in rare-events sampling. This work represents a promising avenue for utilizing quantum computers to address challenging probabilistic modeling problems with improved efficiency and accuracy.
Reference: Blank, C., Park, D.K. & Petruccione, F. Quantum-enhanced analysis of discrete stochastic processes. npj Quantum Inf 7, 126 (2021). ; doi:10.1038/s41534-021-00459-2