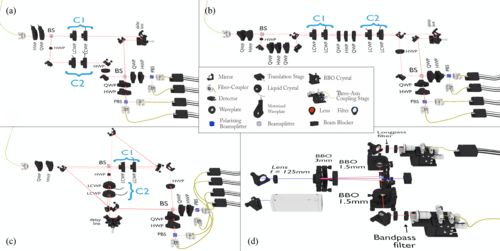
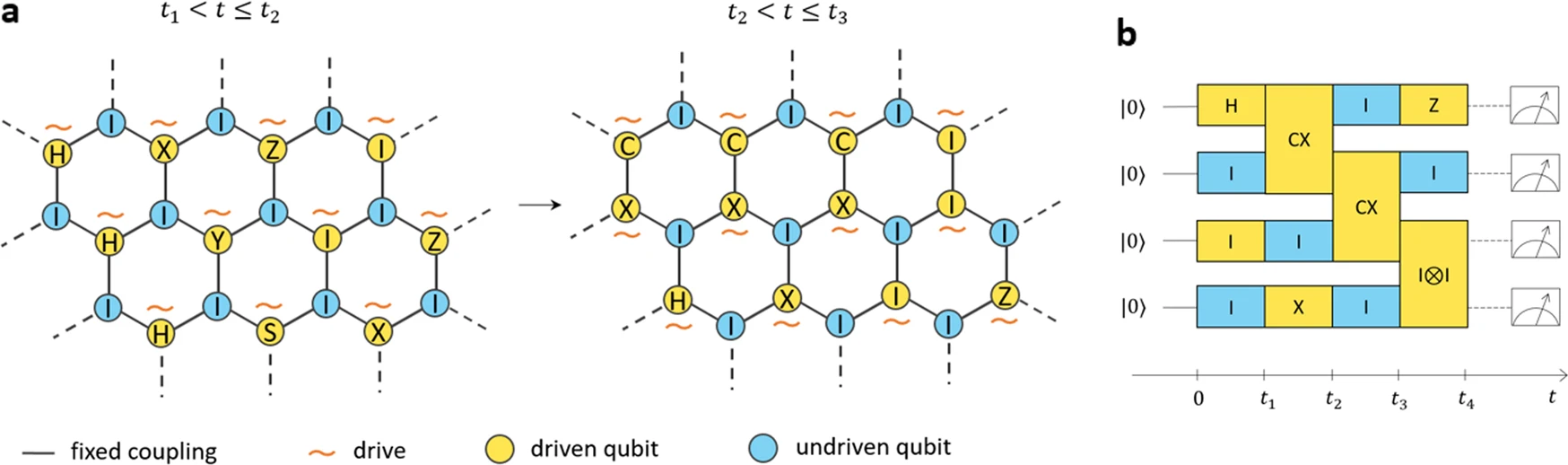
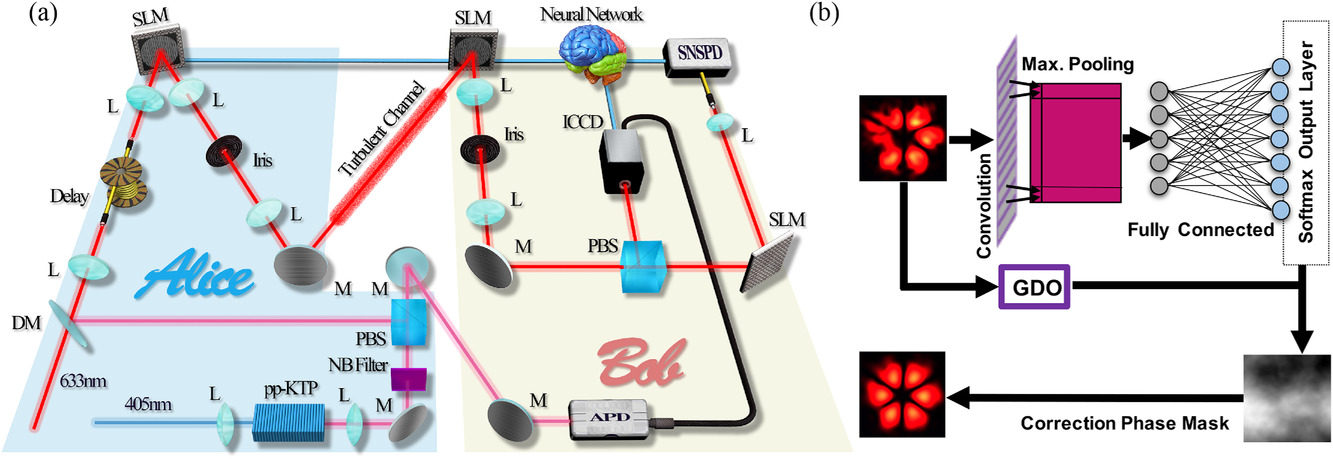
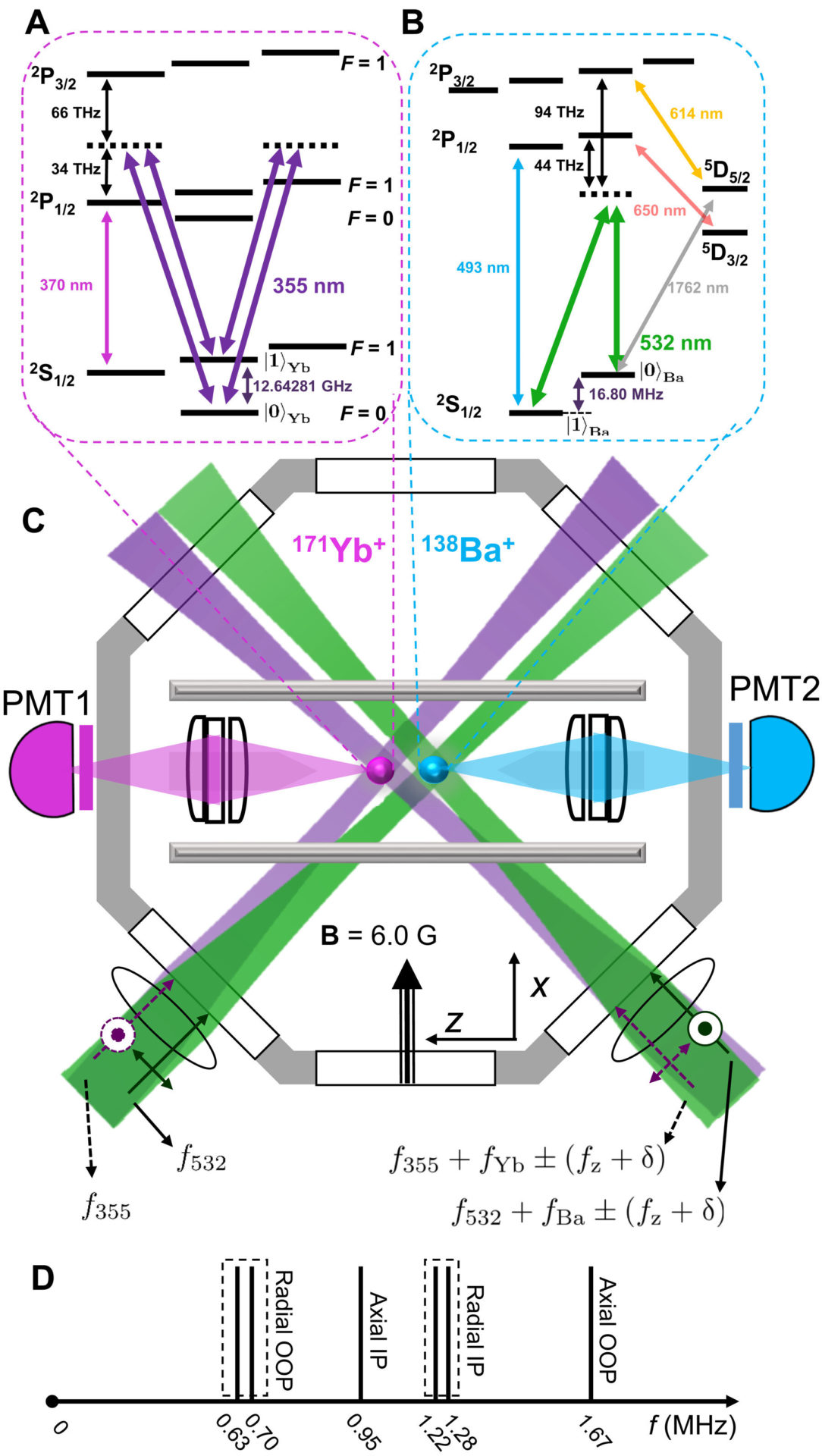
Scientists have shown how three vortices can be linked in a way that prevents them from being dismantled. The structure of the links resembles a pattern used by Vikings and other ancient cultures, although this study focused on vortices in a special form of matter known as a Bose-Einstein condensate. The findings have implications for quantum computing, particle physics and other fields.
Postdoctoral researcher Toni Annala at Aalto University uses strings and water vortices to explain the phenomenon: ‘If you make a link structure out of, say, three unbroken strings in a circle, you can’t unravel it because the string can’t go through another string. If, on the other hand, the same circular structure is made in water, the water vortices can collide and merge if they are not protected.’
The researchers mathematically demonstrated the existence of a structure of linked vortices that cannot break apart because of their fundamental properties. ‘The new element here is that we were able to mathematically construct three different flow vortices that were linked but could not pass through each other without topological consequences. If the vortices interpenetrate each other, a cord would form at the intersection, which binds the vortices together and consumes energy.
The structure is conceptually similar to the Borromean rings, a pattern of three interlinked circles which has been widely used in symbolism and as a coat of arms. A Viking symbol associated with Odin has three triangles interlocked in a similar way. If one of the circles or triangles is removed, the entire pattern dissolves because the remaining two are not directly connected. Each element thus links its two partners, stabilising the structure as a whole.
The mathematical analysis in this research shows how similarly robust structures could exist between knotted or linked vortices. Such structures might be observed in certain types of liquid crystals or condensed matter systems and could affect how those systems behave and develop.
The article has been published in Nature Communication Physics.
Reference: Toni Annala, Roberto Zamora-Zamora, Mikko Möttönen. Topologically protected vortex knots and links. Communications Physics, 2022; 5 (1) DOI: 10.1038/s42005-022-01071-2