Researchers have proposed a quantum implementation of the Stochastic Series Expansion (SSE) Monte Carlo method and shown it offers significant advantages over classical implementations of SSE.
In particular, for problems where classical SSE encounters the sign problem, the cost of implementing a Monte Carlo iteration scales only linearly with system size in quantum SSE, while it may scale exponentially with system size in classical SSE.
In cases where classical SSE can be efficiently implemented, quantum SSE still offers an advantage by allowing for more general observables to be measured.
Quantum Monte Carlo methods have evolved to be indispensable in the study of strongly correlated many-body systems where the interplay between competing interactions result in quantum phases that are not observed in their non-interacting counterparts. In the study of strongly correlated systems, computational methods are vital, as standard analytical techniques based on single particle picture or perturbation theory are often rendered ineffective. Among the different numerical techniques, quantum Monte Carlo methods have proven to be very powerful for their ability to simulate a wide range of realistic microscopic Hamiltonians on relatively large system sizes at all temperatures and in all dimensions.
The phenomenal development of quantum information theory over the past two decades and the advent of quantum computers in the past couple of years have significantly broadened the potential for simulating strongly interacting quantum many-body systems. The ability to represent superposition of states directly on a quantum computer promises exponential speedup of quantum algorithms over their classical counterparts. Algorithms that exploit quantum hardware to speed up simulations of the thermal Gibbs state of many-body systems have previously been explored, but we are still at a nascent stage of harnessing the power of quantum computation in studying correlated systems.
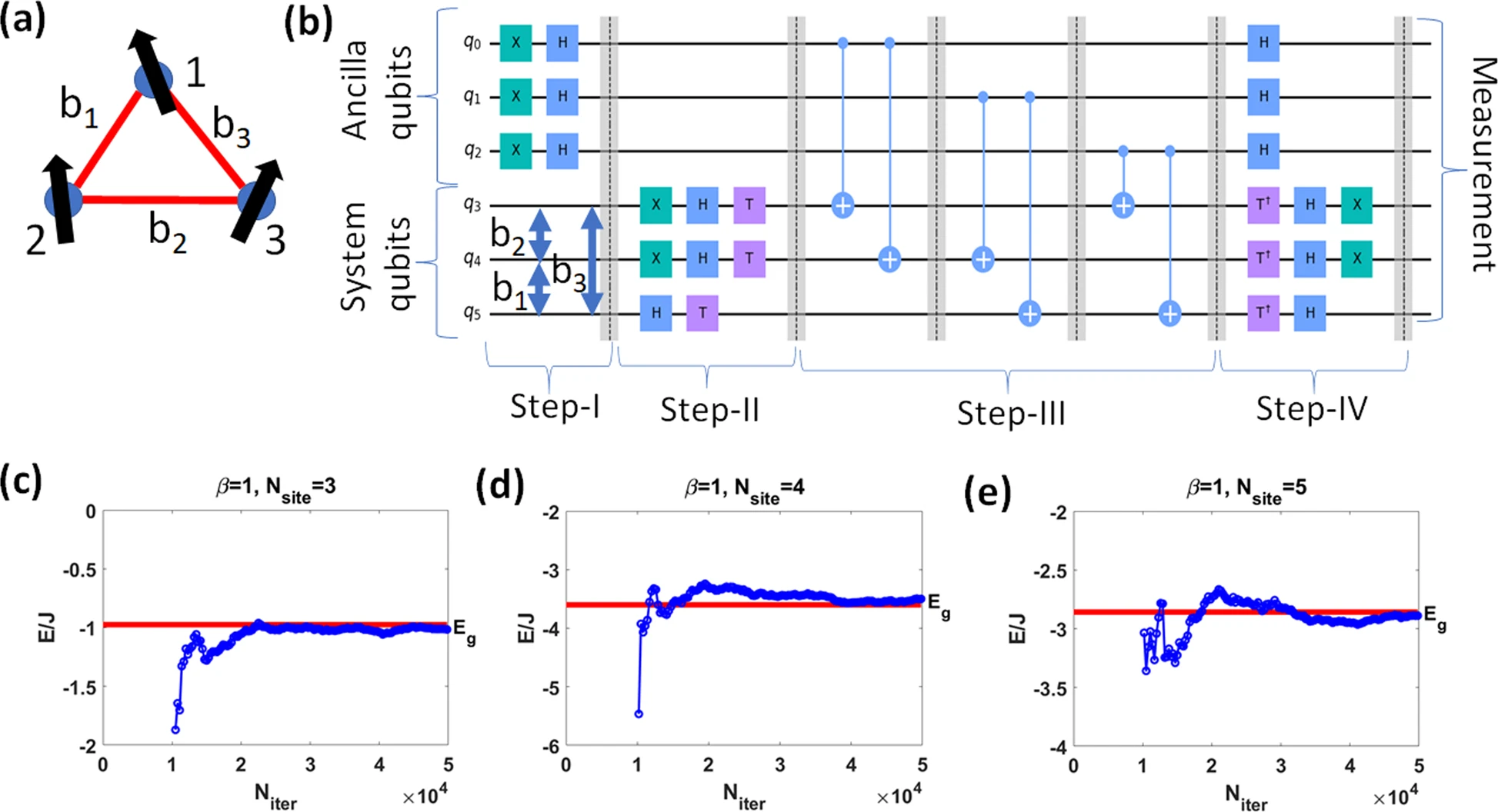
The Stochastic Series Expansion (SSE) method is a widely used Quantum Monte Carlo (QMC) method for simulating models of quantum many-body systems. It is based on sampling the series expansion of exp(−𝛽𝐻) up to a sufficiently high order. A significant advantage of SSE is that expectation values that are obtained via this method are exact, up to statistical errors. Other approaches include the world line method, and the Density Matrix Renormalization Group (DMRG) method.
The team of scientists has proposed an implementation of SSE on a quantum computer and compared its efficiency to conventional SSE on a classical computer. They refer to the former as quantum SSE and the latter as classical SSE and demonstrate several advantages that quantum SSE has over classical SSE. In particular, it has been argued that the no-branching requirement from classical SSE can be relaxed in quantum SSE, which leads to important consequences for the simulation of many-body systems. This quantum advantage stems from the ability of quantum processors to prepare nontrivial superpositions of quantum states. In the subsequent discussion, it is assumed the simulated object is a quantum many-body system with N particles and k-local interactions.
The work has been published in npj Quantum Information.