Quantum Approximate Optimization Algorithm (QAOA) is one of the most promising quantum algorithms for the Noisy Intermediate-Scale Quantum (NISQ) era.
The Quantum Approximate Optimization Algorithm is a hybrid quantum-classical algorithm designed to solve combinatorial optimization problems. It works by preparing a quantum state through a sequence of quantum operations, alternating between two types of unitary transformations: one based on the problem Hamiltonian and another based on a mixing Hamiltonian. The algorithm uses classical optimization to find the best parameters for these transformations.
While QAOA may not always find the optimal solution, it can find good approximate solutions, making it particularly interesting for near-term quantum computers with limited coherence times. The algorithm’s performance typically improves as more iterations are added.
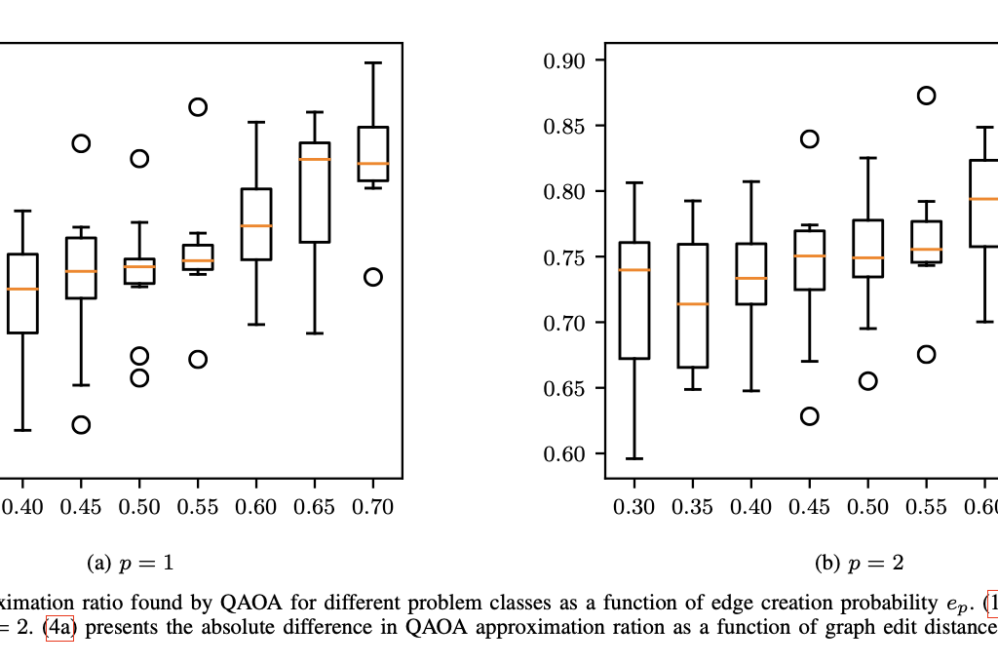
Quantifying the performance of QAOA in the near-term regime is of utmost importance. A team at Argonne National Laboratory and Clemson University in USA has performed a large-scale numerical study of the approximation ratios attainable by QAOA.
To find good QAOA parameters they performed 990 million 10-qubit QAOA circuit evaluations. The researchers found that the approximation ratio increases only marginally as the depth is increased, and the gains are offset by the increasing complexity of optimizing variational parameters. They observed a high variation in approximation ratios attained by QAOA, including high variations within the same class of problem instances. They also discovered that the difference in approximation ratios between problem instances increases as the similarity between instances decreases.