npj Quantum Information, Published online: 06 November 2024; doi:10.1038/s41534-024-00900-2
Classification of dynamical Lie algebras of 2-local spin systems on linear, circular and fully connected topologies
Much is understood about 1-dimensional spin chains in terms of entanglement properties, physical phases, and integrability.
However, the Lie algebraic properties of the Hamiltonians describing these systems remain largely unexplored.
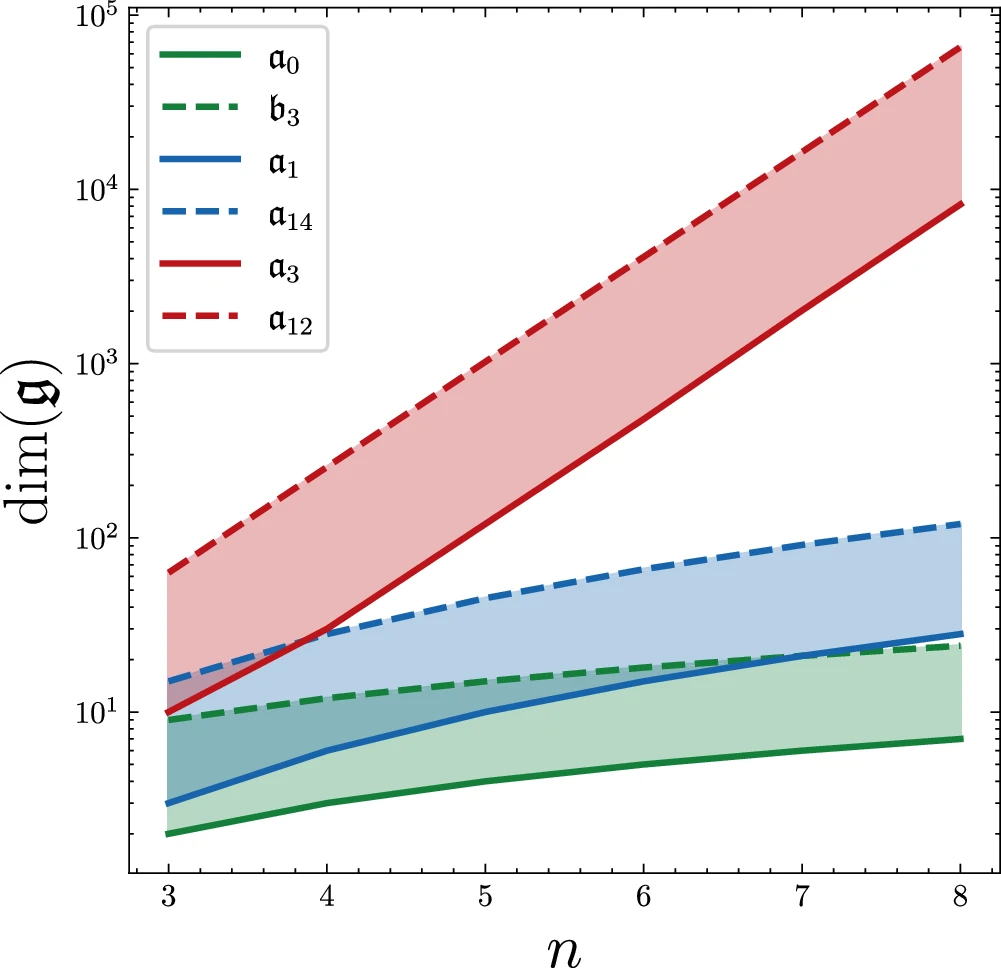
In this work, the team of researchers provide a classification of all Lie algebras generated by the terms of 2-local spin chain Hamiltonians, or so-called dynamical Lie algebras, on 1-dimensional linear and circular lattice structures. They have found 17 unique dynamical Lie algebras. This classification includes some well-known models such as the transverse-field Ising model and the Heisenberg chain, and they also found more exotic classes of Hamiltonians that appear new.
In addition to the closed and open spin chains, they have considered systems with a fully connected topology, which may be relevant for quantum machine learning approaches.
The paper discusses the practical implications of this work in the context of variational quantum computing, quantum control and the spin chain literature.