Quantum computers promise not only to outperform classical machines for certain important tasks, but also to preserve privacy of computation.
For example, the blind quantum computing protocol enables secure delegated quantum computation, where a client can protect the privacy of their data and algorithms from a quantum server assigned to run the computation.
However, this security comes with the practical limitation that the client and server must communicate after each step of computation. A practical alternative is homomorphic encryption, which does not require any interactions, while providing quantum-enhanced data security for a variety of computations.
In this scenario, the server specifies the computation to be performed, and the client provides only the input data, thus enabling secure noninteractive computation.
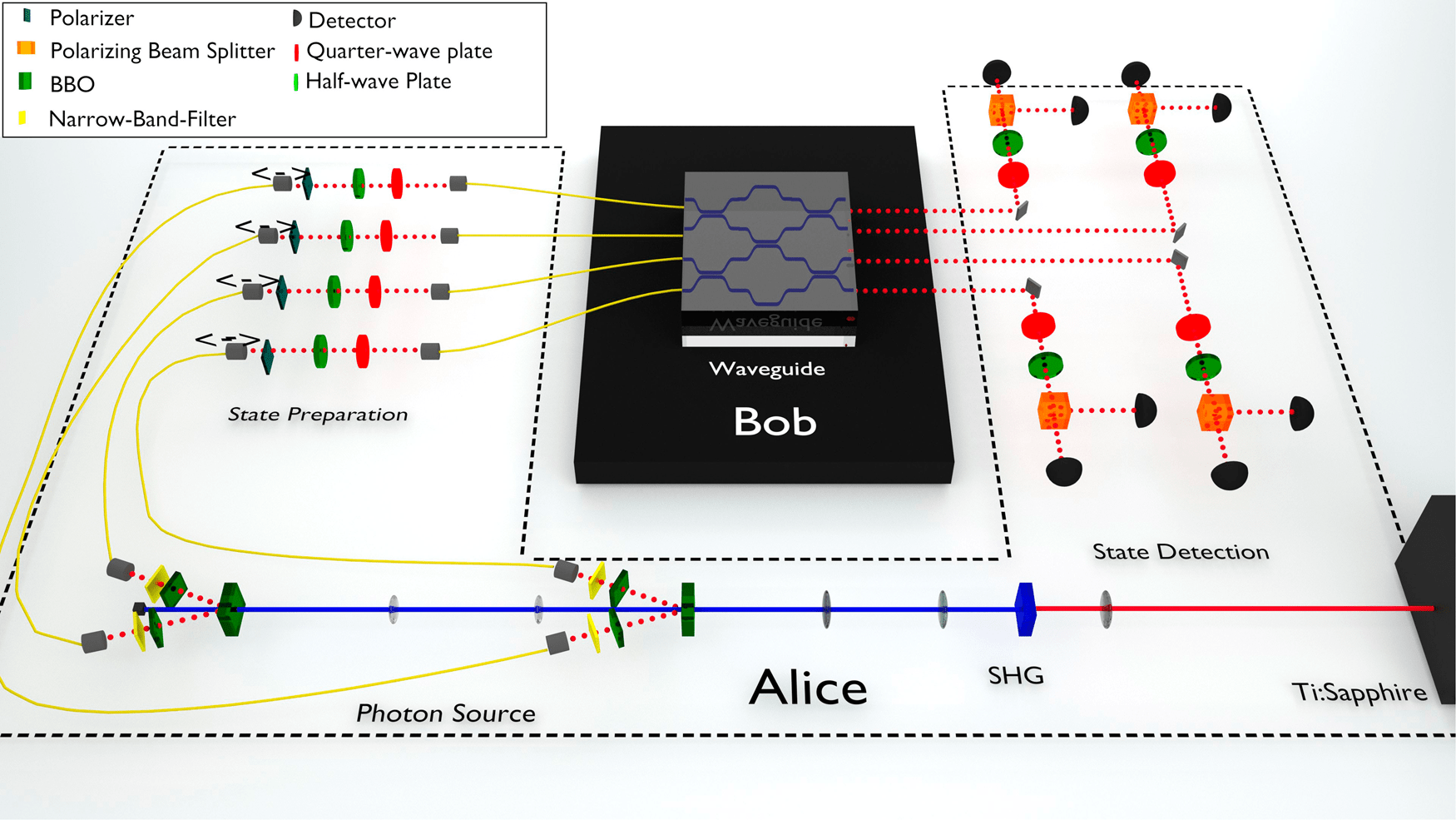
A team of researchers at Vienna Center for Quantum Science and Technology (VCQ) and Centre for Quantum Technologies, Singapore (CQT), has demonstrated homomorphic-encrypted quantum computing with unitary transformations of individual qubits, as well as multi-qubit quantum walk computations using single-photon states and non-birefringent integrated optics. The client encrypts their input in the photons’ polarization state, while the server performs the computation using the path degree of freedom.
This demonstration using integrated quantum photonics underlines the applicability of homomorphic-encrypted quantum computations, and shows the potential for delegated quantum computing using photons.
Secure delegated computing has been a longstanding research goal for both the classical and quantum computation communities. The aim is to provide a client (Alice) access to remote computational resources (Bob), while protecting the privacy of Alice’s data and Bob’s algorithm. In his seminal 2009 paper, Gentry described the first computationally secure, fully homomorphic encryption scheme for classical computing1. Here, “computational security” means that the privacy guarantees of the protocol are based on assumptions about an adversary’s computational capabilities; “fully” means that any computation is possible. Blind quantum computation was also introduced in 2009 (refs. 2,3): this protocol addresses a different situation, in which the data and algorithm both belong to Alice, who wants to use Bob’s remote computational resources without revealing them. Blind quantum computation has the advantages of being information-theoretically secure (i.e., it does not rely on assumptions about the adversary’s technological capabilities) and allowing multiple rounds of communication between Alice and Bob over the course of the computation. Its efficiency is limited by the need for interaction: Alice and Bob must exchange classical information after each step of the computation. Quantum homomorphic encryption—where, in contrast to the scheme of ref. 1, a quantum computation is performed on quantum information—removes the requirement of interactive computation, but necessarily sacrifices either security or computational power to achieve this, in accordance with a no-go theorem: fully homomorphic encryption is impossible if both perfect privacy and non-exponential resource overhead are required4,5.
The paper has been published in npj quantum information.
The post Experimental quantum homomorphic encryption appeared first on Swiss Quantum Hub.