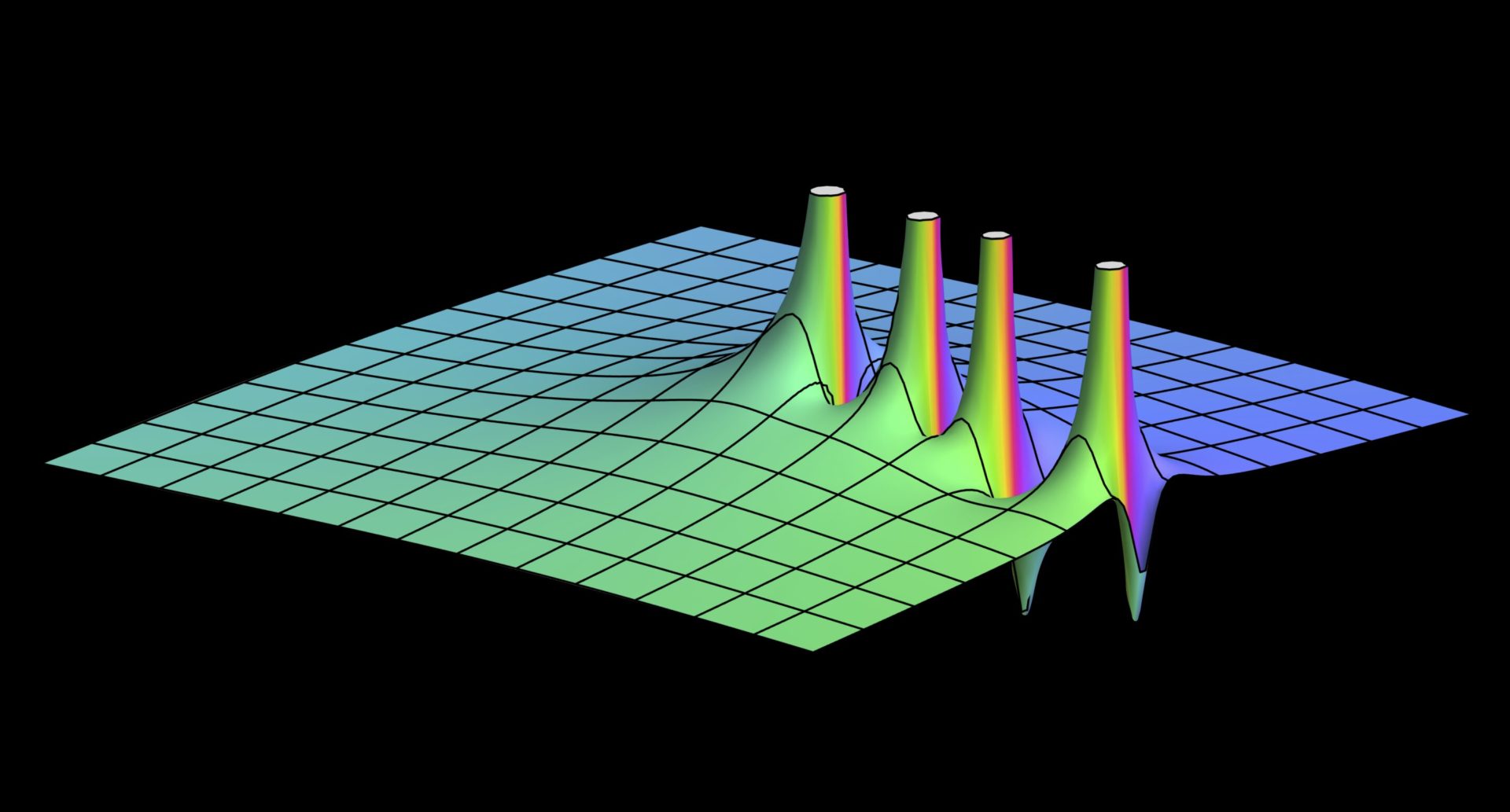
The Riemann zeta function is a deceptively straightforward function that has perplexed mathematicians since the 19th century. The most famous quandary, the Riemann hypothesis, is perhaps the greatest unsolved question in mathematics, with the Clay Mathematics Institute offering a $1 million prize for a correct proof.
Grant Remmen, a quantum field theory scientist at UC Santa Barbara, has found a new approach for exploring the quirks of the famous zeta function.
At its core, the zeta function generalizes the harmonic series:
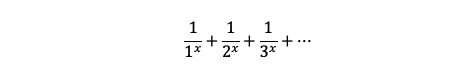
This series blows up to infinity when x ≤ 1, but it converges to an actual number for every x > 1.
Remmen realized one of the concepts therein shares many characteristics with the Riemann zeta function. It’s called a scattering amplitude, and it encodes the quantum mechanical probability that particles will interact with each other. He was intrigued.
His work could even lead to a proof of the Riemann hypothesis.
The paper has been published in Physical Review Letters.