Quantum computation for molecular and material energy calculations represents one of quantum computing’s most promising applications. This research introduces a novel approach for solving ground-state chemistry problems using first quantization with any basis set, advancing beyond previous limitations.
Traditional quantum algorithms have primarily employed second quantization with compact basis sets, while existing first quantization methods were restricted to grid-based approaches. The presented method overcomes these limitations by implementing quantum phase estimation with qubitization for first quantization using arbitrary basis sets.
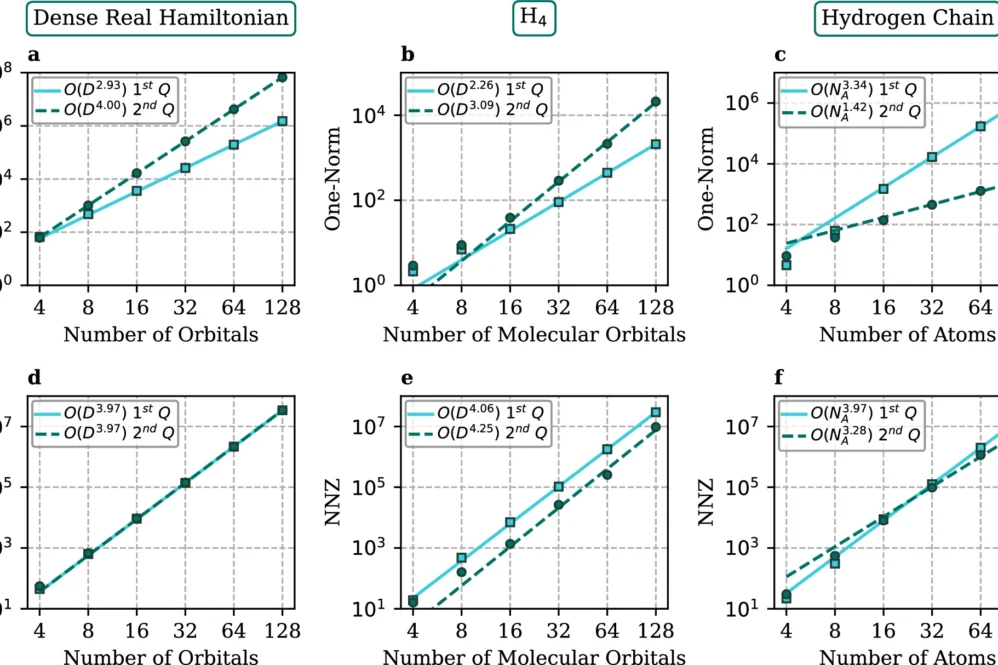
The research demonstrates significant advantages over previous approaches. For molecular orbital calculations, the method achieves asymptotic speedup in Toffoli gate count compared to second quantization methods. When using dual plane waves, it shows orders of magnitude improvements in efficiency. Remarkably, in certain scenarios, this approach matches or even outperforms previous first quantization plane wave algorithms that avoided classical data loading entirely.
A key innovation is the development of the first explicit linear-combination-of-unitaries decomposition in first quantization, utilizing sparse Hamiltonian representation. While focused on electronic structures, the methodology applies broadly to any first quantization Hamiltonian.
The first quantization approach offers substantial advantages, including exponentially reduced qubit requirements when scaling with orbital count, making it particularly valuable for reaching continuum limits with minimal qubit increase. Additionally, unlike second quantization methods, this approach applies equally to bosonic and fermionic systems with fixed particle numbers.
This groundbreaking research represents a significant advancement in quantum computational chemistry by bridging theoretical capabilities with practical implementation. By enabling first quantization approaches with arbitrary basis sets, the work overcomes fundamental limitations of previous methods and establishes a more efficient pathway toward practical quantum advantage for molecular simulations. The demonstrated resource reductions—both in qubit count and gate operations—address critical bottlenecks in quantum chemistry calculations, potentially bringing complex molecular and material systems within reach of near-term fault-tolerant quantum computers. Beyond the immediate applications in chemistry, this methodology provides a foundation for future quantum algorithms across various domains requiring efficient representation of many-body systems. As quantum hardware continues to advance, this approach positions the field closer to achieving practical quantum advantage for problems of genuine scientific and industrial significance.
Reference: Georges, T.N., Bothe, M., Sünderhauf, C. et al. Quantum simulations of chemistry in first quantization with any basis set. npj Quantum Inf 11, 55 (2025). doi:10.1038/s41534-025-00987-1