Por: Camila Pontes (co-fundadora Brazil Quantum)
Introdução
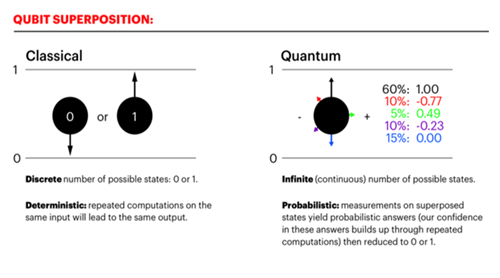
Como conversamos nos últimos posts, o qubit é a parte fundamental da mudança do computador quântico em relação ao computador normal. Desse modo, saber manipulá-lo é parte fundamental do desenvolvimento dessa tecnologia. Por isso, nós da Brazil Quantum queremos lhe mostrar mais uma ferramenta no entendimento do Qubit, a sua representação em Esfera de Bloch!
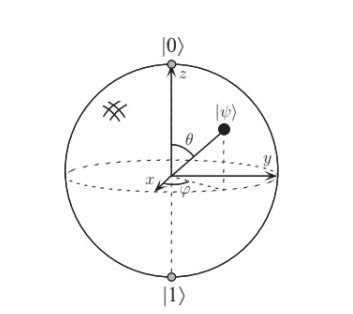
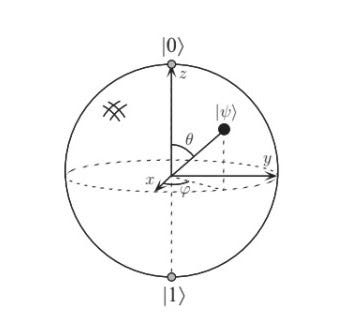
A Esfera de Bloch é uma representação geométrica de um sistema quântico com dois níveis (como o nosso qubit). O polo norte e o polo sul da esfera são os vetores bases |0> e |1> respectivamente, que também poderiam representar um elétron com spin positivo ou negativo quando fazemos um paralelo com a física clássica.
Dado uma base ortonormal, qualquer estado puro ψ de um qubit pode ser escrito como a superposição dos vetores base |0> e |1>, onde o coeficiente de cada componente é um número complexo. Contudo, como a fase relativa entre esses vetores bases é desprovida de significado físico, podemos adotar o coeficiente de |0> como um real não negativo. Desse modo, podemos descrever |ψ> como:
|ψ> = cos(θ/2) |0> + exp(iø)sin(θ/2)|1>
Onde 0 ≤ θ ≤ π e 0 ≤ ø ≤ 2π e esses ângulos definem o ponto na esfera tridimensional que representa o estado físico, como observamos na imagem abaixo.
Gates
Da mesma forma que computadores clássicos são construídos baseados em gates lógicos, computadores quânticos utilizam os chamados quantum gates para transformar o estado físico de um qubit em outro estado. Por exemplo, um gate NOT clássico, que transforma um bit 1 em 0 e vice e versa pode ser definido na computação quântica como sendo um gate que transforma |0> em |1> e |1> em |0>. Mas e no caso de um estado em superposição? Na realidade, visto a característica linear da mecânica quântica, a transformação também é linear. Logo, um estado |0> + |1> é transformado em |1> + |0> pelo nosso NOT quântico.
Os gates quânticos podem ser escritos de maneira conveniente em forma de matriz. No caso do NOT quântico, essa matriz é chamada de X (Já vamos entender o motivo) e é representada como
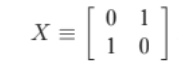
Como você deve se lembrar, podemos representar um Qubit por um vetor de números complexos e módulo unitário. Portanto, aplicar um gate em um qubit nada mais é do que multiplicar o esse vetor pela matriz do gate, como a seguir:
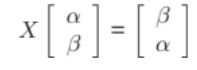
Perceba que, devido a exigência do Qubit ser um vetor unitário, a aplicação de um gate não pode mudar o módulo do nosso vetor. Por esse motivo, quantum gates devem necessariamente ser matrizes unitárias. Se você não se lembra, matrizes unitárias são aquelas que multiplicadas pela sua transposta conjugada resultam na matriz identidade.
O gate X apresentado é o que chamamos de single qubit gates, pois transformam apenas um qubit. Existem alguns single qubit gates importantes e podemos ver suas matrizes abaixo:
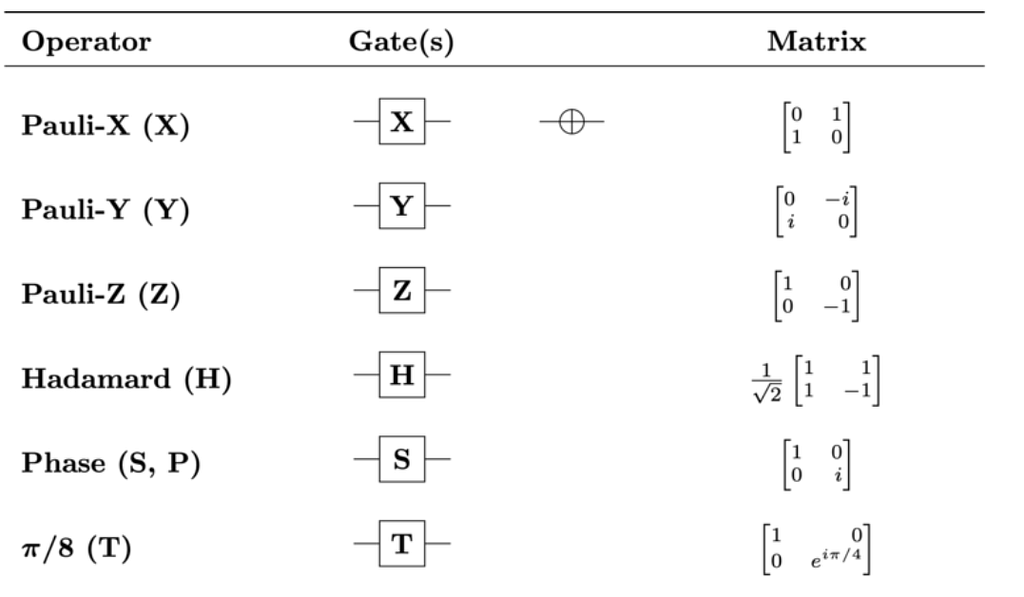
Por fim, a esfera de Bloch apresentada acima é uma ferramenta muito útil para visualizarmos o efeito que um gate tem sobre o estado de um qubit. O gate X, por exemplo, nada mais é do que uma rotação do estado do qubit em torno do eixo X da esfera. O mesmo acontece para os gates Y e Z. Podemos a baixo ver a transformação de qubit quando aplicamos o gate Y:
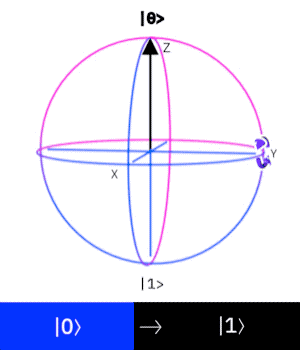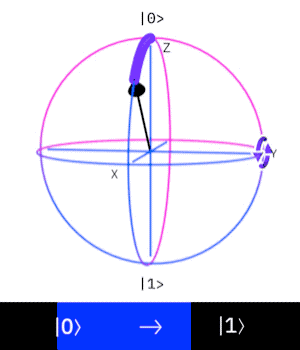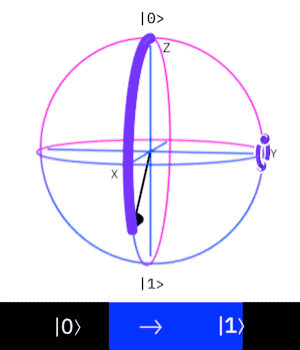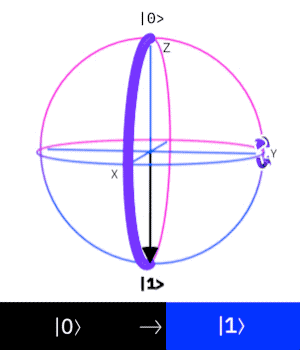
Em um próximo texto, iremos expandir nossos gates para multiple qubits gates, que seguem os mesmos princípios porém agindo sobre mais de um qubit por vez. E em seguida, começaremos a ver que algoritmos quânticos nada mais são do que aplicações sequências de gates de forma que possamos calcular algum resultado desejável. Até lá, sugerimos que você se divirta um pouco com os gates apresentados e tente visualizar na esfera de Bloch o efeito que cada um deles tem e em breve teremos um tutorial no Github para você praticar!
Referências:
Quantum Computation and Quantum Information: 10th Anniversary Edition, de Nielsen, Michael A., Chuang, Isaac L.