Ensuring the correct functioning of Quantum Error Correction (QEC) circuits is crucial to achieve fault tolerance in realistic quantum processors subjected to noise.
The first checkpoint for a fully operational QEC circuit is to create Genuine Multipartite Entanglement (GME) across all subsystems of physical qubits.
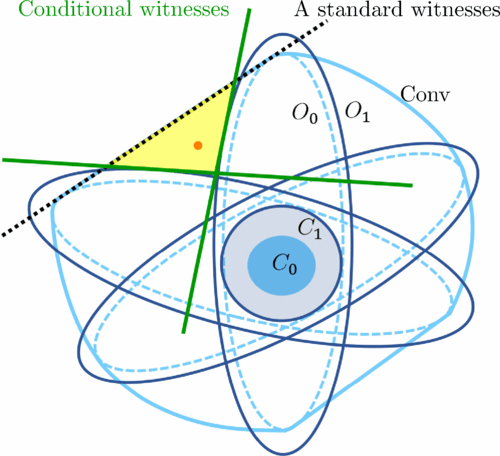
A team of researchers has introduced a conditional witnessing technique to certify GME that is efficient in the number of subsystems and, importantly, robust against experimental noise and imperfections.
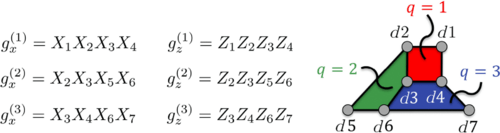
Specifically, they proved that the detection of entanglement in a linear number of bipartitions by a number of measurements that also scales linearly, suffices to certify GME.
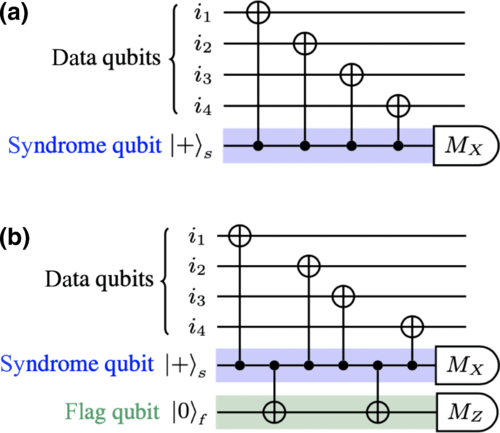
Moreover, their method goes beyond the standard procedure of separating the state from the convex hull of biseparable states, yielding an improved finesse and robustness compared to previous techniques. They have applied their method to the noisy readout of stabilizer operators of the distance-three topological color code and its flag-based fault-tolerant version.
In particular, they subjected the circuits to combinations of three types of noise, namely, uniform depolarizing noise, two-qubit gate depolarizing noise, and bit-flip measurement noise. They numerically compared their method with the standard, yet generally inefficient, fidelity test and to a pair of efficient witnesses, verifying the increased robustness of their method.
Last but not least, they have provided the full translation of this analysis to a trapped-ion native gate set that makes it suitable for experimental applications.
The paper has been published in PRX Quantum.