npj Quantum Information, Published online: 04 October 2024; doi:10.1038/s41534-024-00887-w
Gibbs state sampling via cluster expansions
Gibbs states (i.e., thermal states) can be used for several applications such as quantum simulation, quantum machine learning, quantum optimization, and the study of open quantum systems.
Moreover, semi-definite programming, combinatorial optimization problems, and training quantum Boltzmann machines can all be addressed by sampling from well-prepared Gibbs states.
With that, however, comes the fact that preparing and sampling from Gibbs states on a quantum computer are notoriously difficult tasks. Such tasks can require large overhead in resources and/or calibration even in the simplest of cases, as well as the fact that the implementation might be limited to only a specific set of systems.
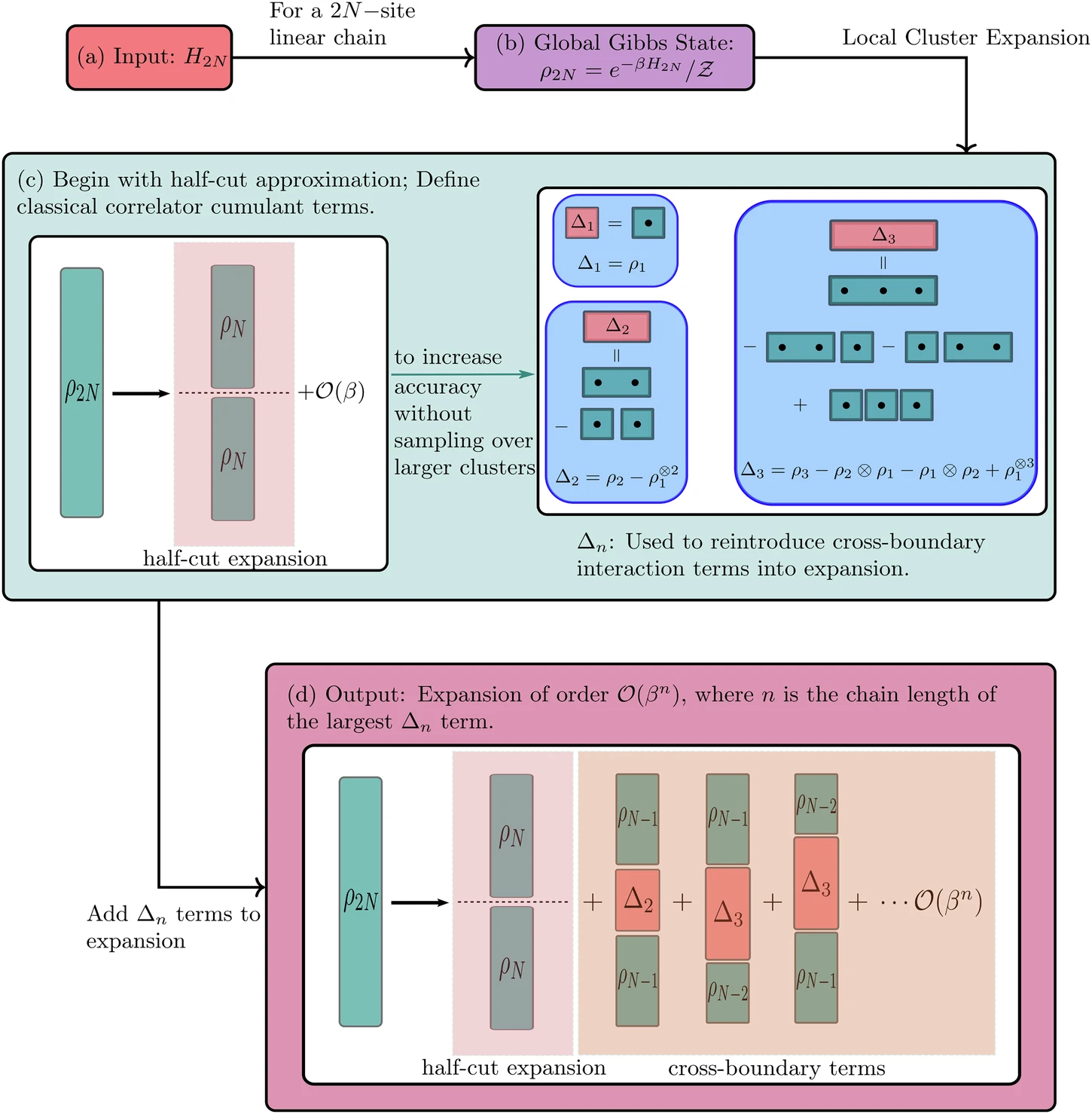
Researchers have proposed a method based on sampling from a quasi-distribution consisting of tensor products of mixed states on local clusters, i.e., expanding the full Gibbs state into a sum of products of local “Gibbs-cumulant” type states easier to implement and sample from on quantum hardware.
They have begun with presenting results for 4-spin linear chains with XY spin interactions, for which they obtained the ZZ dynamical spin-spin correlation functions and dynamical structure factor.
They have also presented the results of measuring the specific heat of the 8-spin chain Gibbs state ρ8.