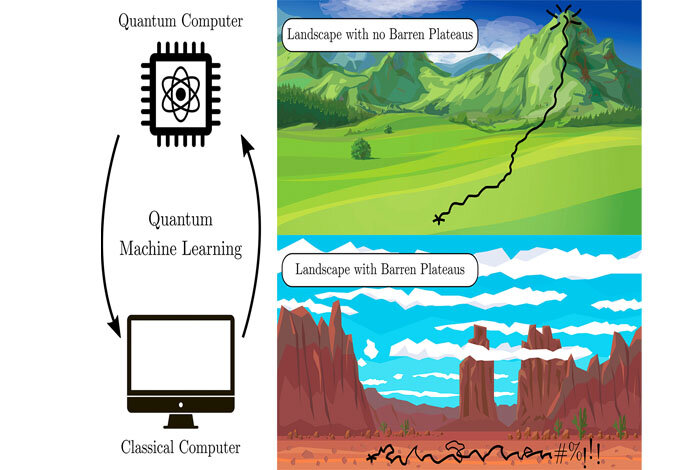
Many machine learning algorithms on quantum computers suffer from the dreaded “barren plateau” of unsolvability, where they run into dead ends on optimization problems.
Researchers at Los Alamos National Laboratory have established theorems that guarantee whether a given machine learning algorithm will work as it scales up on larger computers.
The team used the common hybrid approach for variational quantum algorithms, training and optimizing the parameters on a classical computer and evaluating the algorithm’s cost function, or the measure of the algorithm’s success, on a quantum computer.
Machine learning algorithms translate an optimization task into a cost function. That’s a mathematical description of a function that will be minimized. The function reaches its minimum value only if you solve the problem.
A Variational Quantum Algorithm (VQA) sets up a problem-solving landscape where the peaks represent the high energy points of the system, or problem, and the valleys are the low energy values. The answer lies in the deepest valley. That’s the ground state, represented by the minimized cost function. To find the solution, the algorithm trains itself about the landscape, thereby navigating to the low spot. (Phys.org)
The paper has been published in Nature Communications.