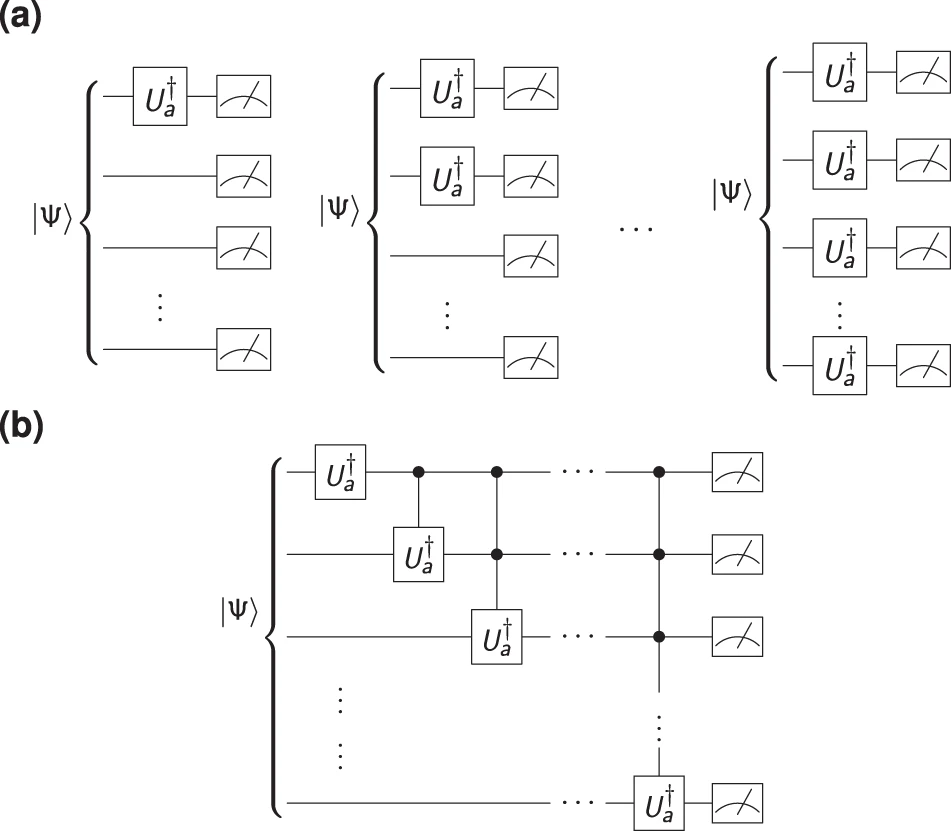
Researchers have introduced an inductive n-qubit pure-state estimation method based on projective measurements on mn + 1 separable bases or m entangled bases plus the computational basis, with m ≥ 2. The method exhibits a favorable scaling in the number of qubits compared to other estimation schemes. The use of separable bases makes their estimation method particularly well suited for applications in noisy intermediate-scale quantum computers, where entangling gates are much less accurate than local gates.
Because of the properties of NISQ computers, the design of methods for the characterization, certification, and benchmarking of these quantum devices has become increasingly relevant and difficult. For instance, the characterization of states generated by this class of devices requires measurements on a large set of bases. These are physically implemented by applying sets of universal unitary transformations on the qubits followed by measurements on a computational basis. Typically, an effort to reduce the number of bases leads to a new set of bases that require the application of entangling unitary transformations, such as, for instance, the controlled NOT (CNOT) gate, whose implementation is associated with a large error. Consequently, the estimation of states generated by NISQ devices could be affected by a large build-up of inaccuracy in the measurement procedure.
Several methods have been proposed to assess the performance of NISQ devices. Randomized benchmarking, direct fidelity estimation, and entanglement certification are popular tools for this purpose. However, they do not give complete information about the device in question. In contrast, quantum state estimation gives plenty of information about the device since it fully determines the state of the system from a set of suitably chosen measurements.
Today, several protocols to perform quantum state estimation of d-dimensional quantum systems are available. These attempt to estimate the d2 − 1 real parameter that characterizes density operators. Standard quantum tomography is based upon the measurement of the d2 − 1 generalized Gell-Mann matrices. Quantum state estimation based on projections onto the states of d + 1 mutually unbiased bases has been suggested to reduce the total number of measurement outcomes. This number can be reduced to a minimum using a symmetric, informationally complete, positive operator-valued measure, which has exactly d2 measurement outcomes.
Despite the progress made in the reduction of the total number of measurement outcomes used by quantum state estimation methods, the exponential increase of this number prevails in the case of multipartite systems. This is known as the curse of dimensionality. For example, standard quantum tomography for a n-qubit system requires the measurement of 3n local Pauli settings. A solution to overcome this problem is the use of a priori information about the state to be determined. Compressed sensing allows a large reduction in the total number of measurements as long as the rank of the state is known. Another alternative is to consider states with special properties, such as, for instance, matrix product states or permutationally invariant states, which also leads to a significant reduction in the total number of measurements. The important case of pure states has also been studied. In this case a set of five bases allows one to estimate with high accuracy all pure quantum states. Recently, a 3-bases-based tomographic scheme has been introduced to estimate a single qudit. The generalization of this method to multiple qubits leads to entangled bases. Adaptivity has also been introduced as a means of increasing the estimation accuracy of tomographic methods and even reaching fundamental accuracy limits.
The team presented a method to estimate unknown pure quantum states in n-qubit Hilbert spaces, as used by NISQ computers, by means of mn + 1 local bases (with m an integer number), which correspond to the tensor product of n single-qubit bases, or by the computational basis plus m entangled bases, that is, bases that cannot be decomposed as the tensor product of single-qubit bases. Thereby, the number of bases scales linearly as O(mn) and O(m), respectively, with the number n of qubits. This is a great advantage over standard methods, which are of exponential order. The mn + 1 local bases also provide an advantage in the estimation of states generated via NISQ devices, such as current prototypes of quantum processors, because in this case projective measurements can be carried out without the use of typically noisy entangling gates. The computational basis together with m = 2 entangled bases also leads to a clear reduction with respect to the 5-bases tomographic method. The method here proposed also improves over the 3-bases method, since this requires calculating the likelihood function of 22𝑛−122n−1 states to obtain an estimate. For a large number of qubits, this stage exponentially increases the computational cost of the method. Furthermore, in order to obtain distinguishable values of the likelihood, a large ensemble size is required. Our estimation method does not require such a procedure.
Their method is also capable of estimating the purity of mixed states generated by the action of white noise on pure states. Monte Carlo simulations show that the method achieves a high estimation fidelity. Besides, the fidelity can be improved by increasing m above 2.
They experimentally demonstrated the method on the IBM’s quantum processors by estimating up to 10-qubit separable and entangled states. In particular, a 4-qubit GHZ is estimated with experimental fidelity of 0.875.
The paper has been published in npj Quantum Information.