In the era of Noisy Intermediate-Scale Quantum (NISQ) computers it is crucial to design quantum algorithms which do not require many qubits or deep circuits. Unfortunately, most of the well-known quantum algorithms are too demanding to be run on currently available quantum devices.
Moreover, even the state-of-the-art algorithms developed for the NISQ era often suffer from high space complexity requirements for particular problem classes.
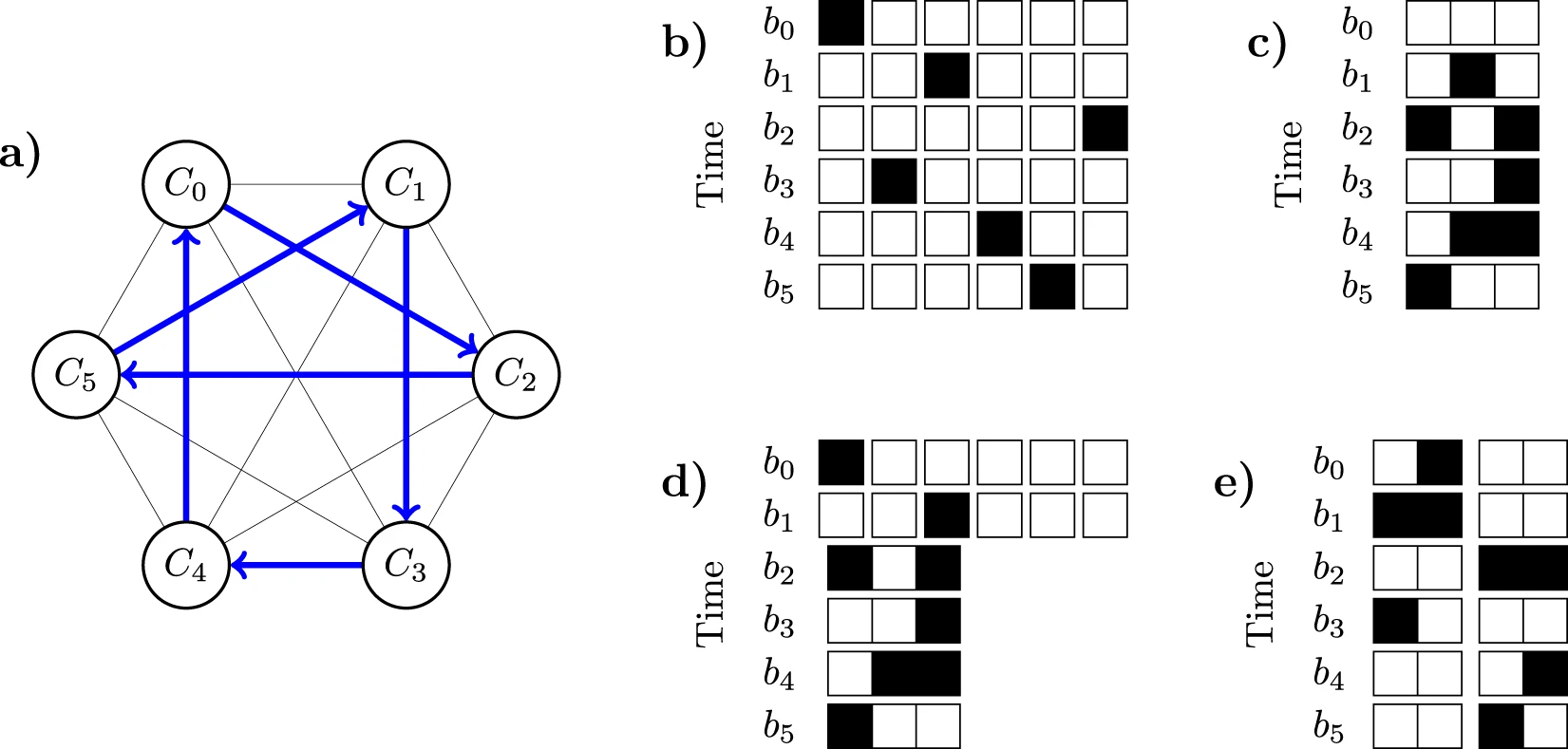
Researchers have showed that it is possible to greatly reduce the number of qubits needed for the Travelling Salesman Problem (TSP), a paradigmatic optimization task, at the cost of having deeper variational circuits.
While the focus is on this particular problem, they claim that the approach can be generalized for other problems where the standard bit-encoding is highly inefficient.
The team also proposes encoding schemes which smoothly interpolate between the qubit-efficient and the circuit depth-efficient models. All the proposed encodings have the same volume up to polylogarithmic factors and remain efficient to implement within the Quantum Approximate Optimization Algorithm framework.
The paper has been published in npj Quantum Information.