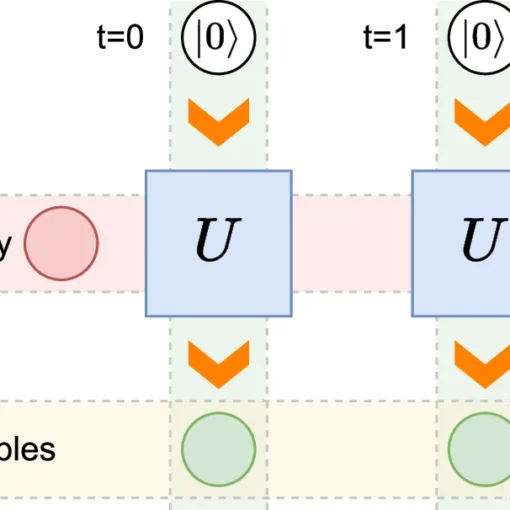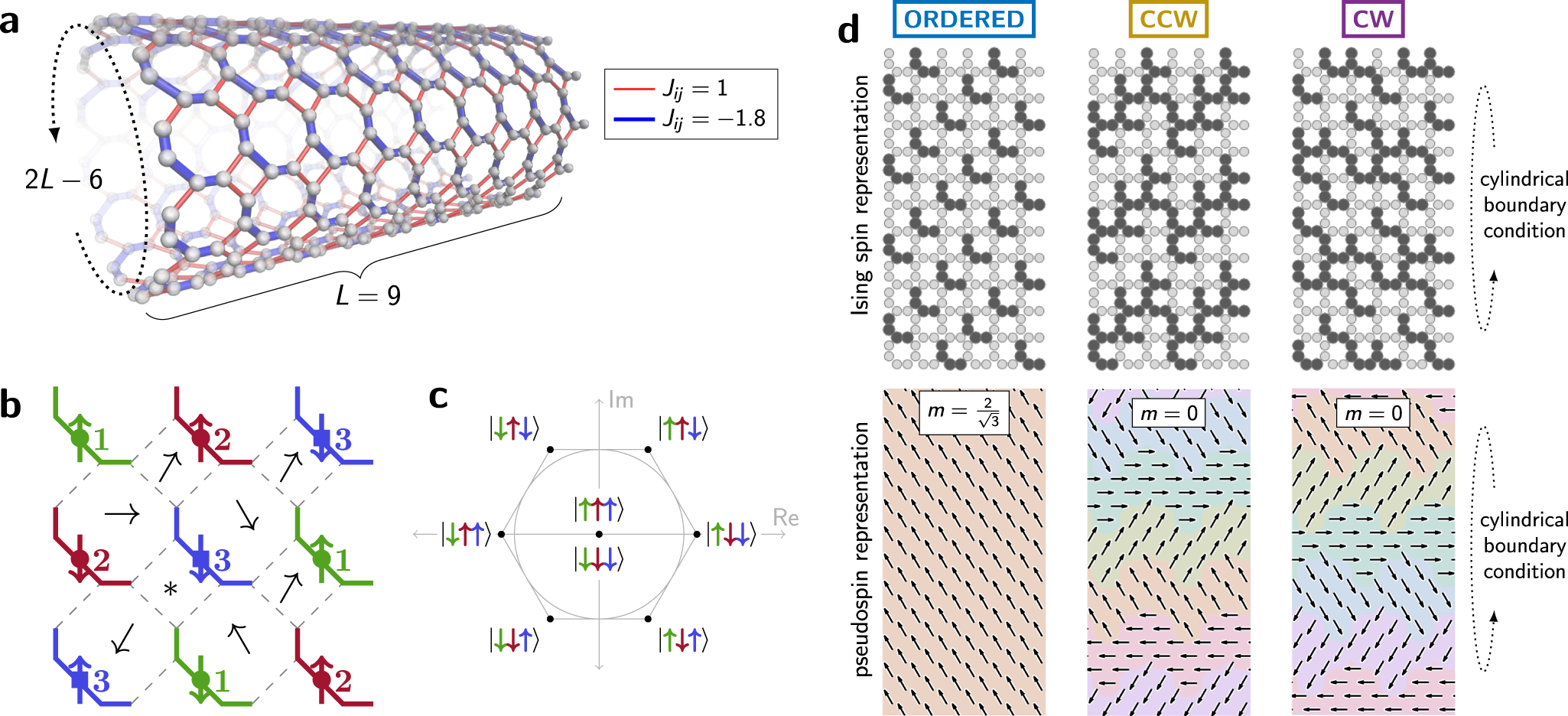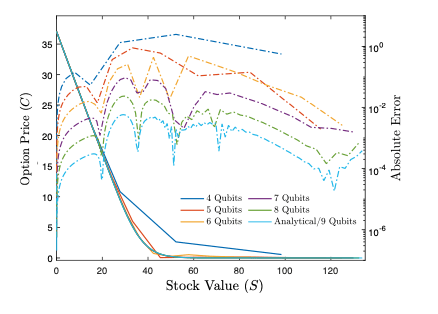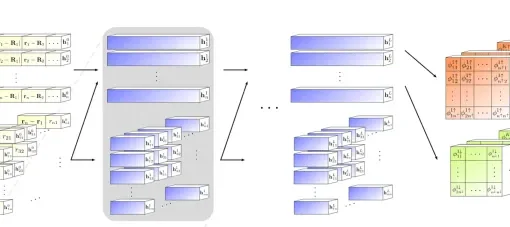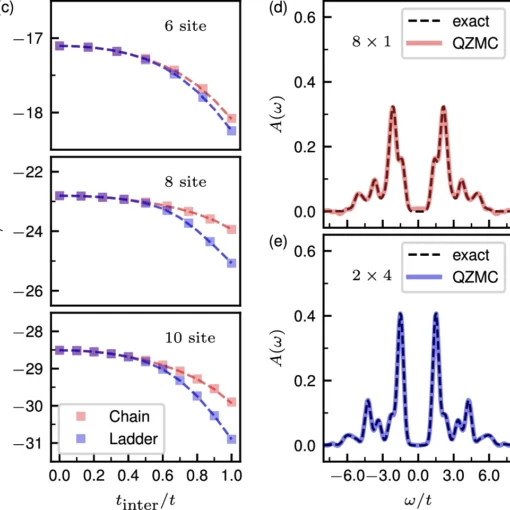
Quantum Zeno Monte Carlo for computing observables
The Quantum Zeno Monte Carlo algorithm bridges the gap between noisy intermediate-scale quantum and fault-tolerant quantum computing eras by offering polynomial computational complexity and resilience to both device noise and Trotter errors without requiring initial state overlap or variational parameters, as demonstrated on IBM’s NISQ devices with up to 12 qubits.