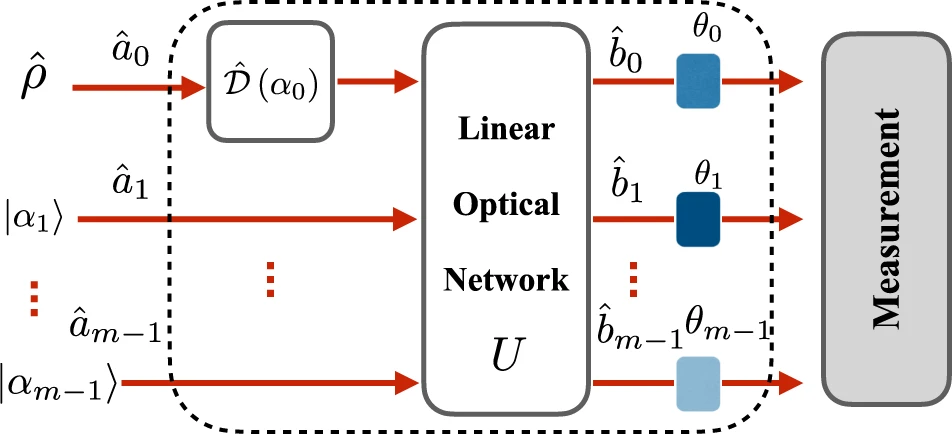
It is well-known that the precision of a phase measurement with a Mach-Zehnder interferometer employing strong classic light can be greatly enhanced with the addition of weak nonclassical light.
In the context of quantifying nonclassicality, the amount by which a nonclassical state can enhance precision in this way has been termed its ’metrological power’. To-date, the enhancement provided by weak nonclassical states has been calculated only for specific measurement configurations.
A team has been able to optimize over all measurement configurations to obtain the maximum enhancement that can be achieved by any single or multi-mode nonclassical state together with strong classical states, for local and distributed quantum metrology employing any linear or nonlinear single-mode unitary transformation.
This analysis reveals that the quantum Fisher information for quadrature-displacement sensing is the sole property that determines the maximum achievable enhancement in all of these different scenarios, providing a unified quantification of the metrological power.
npj Quantum Information, Published online: 11 January 2023; doi:10.1038/s41534-022-00670-9